Моноиды
Моноидом называется тройка (M, #, u), где # - ассоциативная бинарная операция на M, а u - ее единичный элемент.
Моноид полугруппа с нейтральным элементом. m # u = m = u # m
Моноиды
- (Int, +, 0)
- (Int, *, 1)
- (Bool, &&, True)
- (Bool, ||, False)
- (M, min, Top), где M - вполне упорядоченное множество, а Top - его максимальный элемент
- (списки, append, [])
- (множества, объединение, пустое множество)
- (сортированные списки, merge, пустой список)
- (матрицы, умножение, единичная матрица)
Моноиды
- (эндоморфизмы, композиция, тождественная функция), где эндоморфизмом на множестве M называется функция из M в M
- (блоки кода, последовательное выполнение, пустой блок кода)
Моноиды
- Если M1,M2 - моноиды, то M1 x M2 - моноид (декартово произведение множеств, покомпонентное применение #, пара из двух единиц)
- Если # - ассоциативная бинарная операция на M, но единичного элемента среди M нет, то можно его добавить: (M+{e}, #', e), где x #' e = e #' x = x, x#'y = x#y
- Если (M, #, e) - моноид, то (M, @, e) - тоже моноид, где x @ y = y # x - т.н. "двойственный" моноид
- Если (M, #, e) - моноид, то для любого P тотальные функции P->M образуют моноид
(P -> M, \f1 f2 -> \p -> f1 p # f2 p, \p -> e)
Моноиды
- Например, если M - моноид блоков кода, то можно получить моноид (процедуры с параметром P, последовательное выполнение, пустая процедура)
- Аналогично - частичные функции или словари - моноид по объединению
Гомоморфизм моноидов
Если (M, #, e) и (P, @, u) – моноиды, то функция f :: M -> P называется гомоморфизмом между этими двумя моноидами, если f (m1 # m2) = f m1 @ f m2 для всех m1, m2 из M. чему равно u ?
Гомоморфизм моноидов
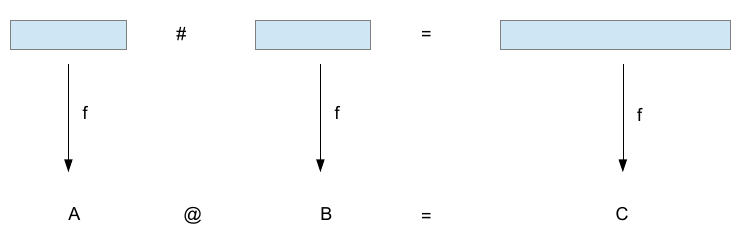
Списочный гомоморфизм
Списочным гомоморфизмом называется гомоморфизм из моноида (списки, append, пустой список) в какой-либо другой моноид.
То есть, функция f называется списочным гомоморфизмом, если существует оператор #, такой, что f (xs ++ ys) = f xs # f ys. Это свойство позволяет независимо вычислить результаты применения функции для подсписков, и собрать из них результат для всего списка при помощи #.
Списочный гомоморфизм
| # | u | f | |
|---|---|---|---|
| sum | + | 0 | \x -> x |
| length | + | 0 | \x -> 1 |
| filter p | ++ | [] | \x -> if (p x) then [x] else [] |
| map f | ++ | [] | \x -> f x |
| sort | merge | [] | \x -> [x] |
Списочный гомоморфизм
Чрезвычайно важно, что благодаря ассоциативности @, в выражении x1 @ x2 @ x3 @ ... @ xn можно расставлять скобки как угодно, вычисляя его в любом порядке (надо, однако, помнить, что @ не обязан быть коммутативным).
Удобство гомоморфизма на списках
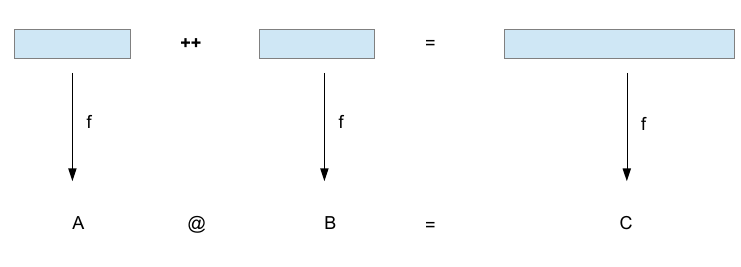
Удобство гомоморфизма на списках
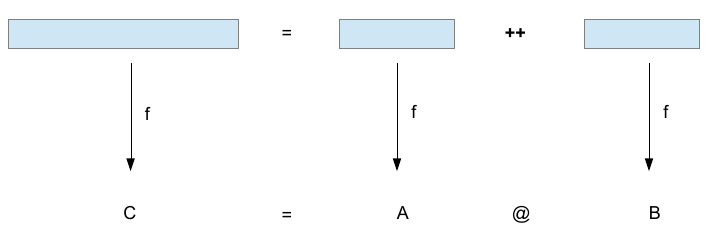
Удобство гомоморфизма на списках
f ~ (map, reduce)
f [x] = map x
reduce A::[] B::[] = A @ B
Гомоморфизм
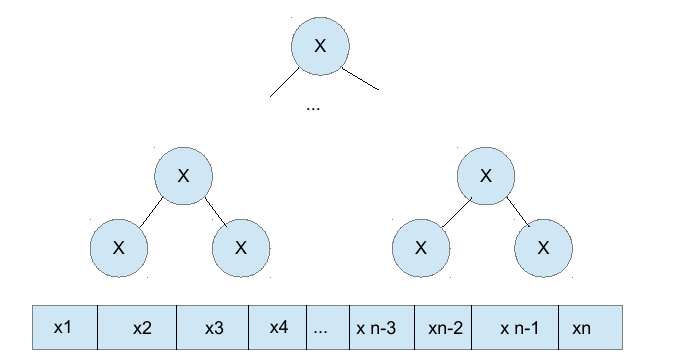
Гомоморфизм
- Позволяет вычислить ответ для N элементов за log N фаз (соответствующих уровням дерева), каждая из которых может быть распараллелена. На P процессорах можно ускорить программу в O(P/logP) раз.
- Позволяет при изменении значения какого-нибудь элемента перевычислить ответ для всего списка за O(log N) операций, изменив только элементы по пути от измененного к корню.
Гомоморфизм
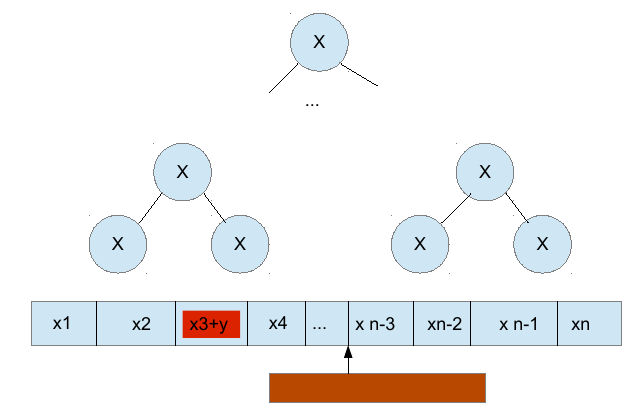
Гомоморфизм
© Евгений Кирпичёв
regEx = /^(a+ b* c)*$/
s0 --a--> s1
s1 --a--> s1
s1 --b--> s2
s1 --с--> s0 // bingo
s2 --b--> s2
s2 --c--> s0 // bingo
s? --?--> s3
Списочный гомоморфизм
regEx = /(a+ b* c)*/| a | b | c | |
|---|---|---|---|
| s0 | s1 | s3 | s3 |
| s1 | s1 | s2 | s0 |
| s2 | s3 | s2 | s0 |
| s3 | s3 | s3 | s3 |
эндоморфизм на S
Списочный гомоморфизм
map x = \s -> fx s -- fx – функция-столбец
reduce f g = f . g| a | b | c | |
|---|---|---|---|
| s0 | s1 | s3 | s3 |
| s1 | s1 | s2 | s0 |
| s2 | s3 | s2 | s0 |
| s3 | s3 | s3 | s3 |
Списочный гомомрфизм
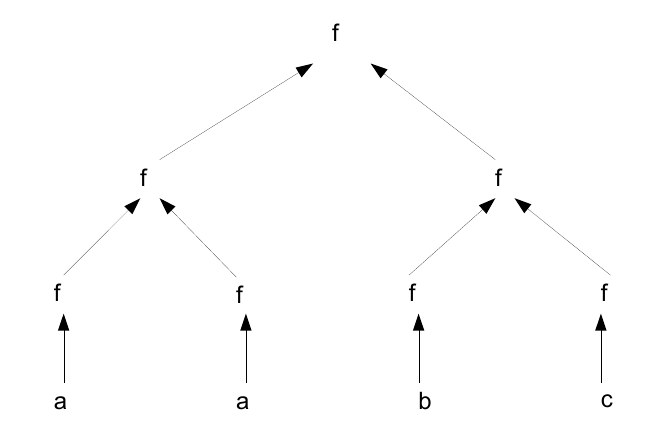
Третья теорема о гомоморфизмах
Если функция f выражается и в виде левой, и в виде правой свертки с одинаковым начальным значением (но, возможно, разной операцией #), то она является списочным гомоморфизмом - и, следовательно, допускает параллельное и инкрементальное вычисление с помощью дерева.
Классы типов
Операция сравнения есть везде, но равны ли наши деревья?
let a = list2tree [1,5,3,2]
a == a?полиморфизм
Классы типов

Классы типов
class Eq a where
(==) :: a -> a -> Bool
Как это работает?
(==) :: (Eq a) => a -> a -> Bool
instance Eq Integer where
x == y = x ‘integerEq‘ y
Классы типов
data Tree a = EmptyTree | Node a (Tree a) (Tree a)
deriving (Show, Read)
instance (Eq a) => Eq (Tree a) where
EmptyTree == EmptyTree = True
(Node a l1 r1) == (Node b l2 r2) =
(a==b) && (l1 == l2) && (r1 == r2)
_ == _ = False
Классы типов
class Eq a where
(==), (/=) :: a -> a -> Bool
x /= y = not (x == y)
class (Eq a) => Ord a where
(<), (<=), (>=), (>) :: a -> a -> Bool
max, min :: a -> a -> a
Классы типов
#==# - списки равны или являются идентичными по перевороту:
[1,2,3] #==# [1,2,3] -- True
[1,1,1] #==# [1,1,2] -- False
[1,2,3] #==# [3,2,1] -- True
Классы типов
class Itch a where
(#==#) :: a -> a -> Bool
instance (Eq a) => Itch [a] where
[] #==# [] = True
x #==# y = (x == reverse y) || (x == y)
Классы типов
lol a b = a #==# b
> :t lol
lol :: Itch a => a -> a -> Bool
Классы типов
#==# - списки являются одинаковыми множествами (Set):
[1,2,3] #==# [1,2,3] -- True
[1,1,1] #==# [1,1,2] -- False
[1,2,3] #==# [3,2,1] -- True
[1,2,2] #==# [2,1,2] -- True
[1,2,2] #==# [1,2] -- True
[1,2,15] #==# [13] -- False